جواب تمرین صفحه ۲۹ و ۳۰ ریاضی یازدهم تجربی

در این نوشته با جواب تمرین صفحه ۲۹ و ۳۰ ریاضی یازدهم تجربی همراه شما هستیم.

جواب تمرین صفحه ۲۹ و ۳۰ ریاضی یازدهم تجربی

۱) الف- دو پاره‌خط AB و CD مطابق شکل داده شده‌اند. نقطه‌ای بیابید که از دو نقطهٔ A و B به یک فاصله باشد و از دو نقطهٔ D و C نیز به یک فاصله باشد.

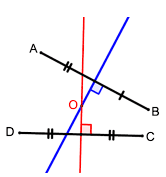
بنا بر خاصیت عمود منصف نقطه ای اکه از دو نقطه ی A و B به یک فاصله باشد روی عمودمنصف پاره خط AB قرار دارد و همچنین نقطه ای که از دو نقطه ی D و C فاصله ثابت دارد روی عمود منصف پاره خط CD قرار دارد.بنا براین جواب مسئله محل برخورد این دو عمود منصف است .

ب- نقطهٔ مورد نظر در قسمت (الف) را O می‌نامیم. اگر نقطهٔ O روی عمودمنصفِ پاره‌خط BC باشد و G دایره‌ای به مرکز O و به شعاع OA باشد، رأس‌های چهارضلعی ABCD نسبت به دایرهٔ G چه وضعیتی دارند؟ چرا؟

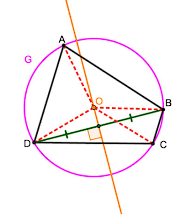
نقطه O روی عمود منصف AB است بنابراین : OB=OA) 1)

نقطه O روی عمود منصف CD است بنابراین : OD=OC) 2)

و با توجه به قسمت (ب) نقطه O روی عمود منصف BC است بنابراین : OB=OC) 3 )

از رابطه های (۱) و (۳) نتیجه می گیریم که : OC=OA) 4 )

از رابطه ی (۴) و رابطه (۲) نتیجه می گیریم که : OD=OC=OB=OA

۲) مثلثی دلخواه رسم کنید و آن را ABC بنامید. عمودمنصف‌های دو ضلع این مثلث را رسم کنید و نقطهٔ برخورد آنها را O بنامید. به مرکز O و به شعاع OAیک دایره رسم کنید. نقاط B و C نسبت به این دایره چه وضعیتی دارند؟ چرا؟

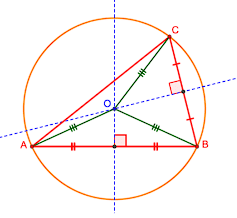
نقاط B و C روی این دایره اند زیرا :

نقطه ی O روی عمود منصف ضلع BC است بنا براین OC=OB) 1)

نقطه ی O روی عمود منصف ضلع AB است بنا براین OB=OA) 2 )

از رابطه های (۱) و (۲) نتیجه می گیریم که : OB=OC=OA پس نقاط B و C نیز باید روی دایره به شعاع OA باشند.

نکته: این دایره ،دایره محیطی مثلث نام دارد و با توجه به مطالب فوق هر مثلث حتما یک دایره ی محیطی دارد.مرکز این دایره محل برخورد عمود منصف های مثلث است و شعاع آن فاصله ی این نقطه از رأس های مثلث است.

نکته

۳) مثلثی دلخواه رسم کنید و آن را ABC بنامید. نیمسازهای دو زاویهٔ این مثلث را رسم کنید و نقطهٔ برخورد آنها را O بنامید. از نقطهٔ O بر سه ضلع مثلث عمود رسم کنید و پای یکی از عمودها را H بنامید. به مرکز O و به شعاع OH دایره‌ای رسم کنید. اضلاع مثلث ABC نسبت به این دایره چه وضعیتی دارند؟ چرا؟

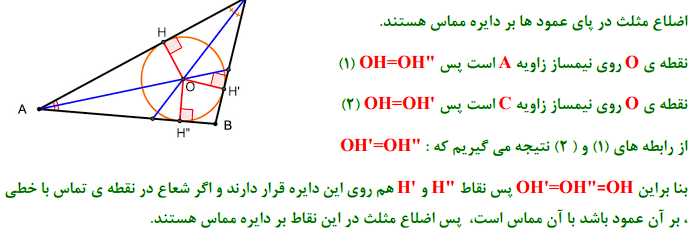
نکته : این دایره، دایرهمحاطیمثلث نام دارد وبا توجه به مطالب فوق هر مثلث حتما یک دایرهمحاطیداخل دارد.که مرکز آن نقطه برخورد نیمساز های داخلی است. و شعاع آن برابر با فاصله ی این نقطه از اضلاع مثلث است.

نکته

۴) فرض کنید نقطهٔ A به فاصلهٔ ۴ سانتی‌متر از خط d باشد. روش رسم هریک از مثلث‌های زیر را توضیح دهید.

الف- مثلثی متساوی‌الساقین که A یک رأس آن و قاعدهٔ آن بر خط d منطبق باشد.

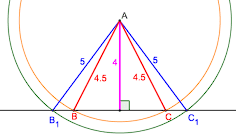
چون می خواهیم مثلث ABC متساوی الساقین باشد به طوری که AC=AB و ضلع BCروی خط d باشد ، پس باید نقاط B و C به فاصله ای مساوی از A و روی خط d باشند. اگر بخواهیم این نقاط از نقطه ی A به یک فاصله باشند باید به مرکز A و شعاع دلخواه دایره رسم کنیم ولی چون می خواهیم که این نقاط روی خط d هم باشند بنا براین شعاع این دایره باید بزرگ تر از ۴ سانتی متر باشد زیرا در غیر اینصورت این دایره خط d را در دو نقطه قطع نمی کند.

نکته : می توان بی شمار مثلث متساوی الساقین با این روش رسم کرد.

نکته

ب- مثلثی که شرایط (الف) را داشته باشد و طول ساق آن ۶ سانتی‌متر باشد.

برای این منظور کافی است به مرکز A و شعاع ۶ سانتی متر که از ۴ بزرگ تر است دایره ای رسم کنیم این دایره خط d را در نقاط B و C قطع می کند و مثلث ABC جواب مسئله است

پ- مثلثی رسم کنید که شرایط قسمت (الف) را داشته باشد و مساحت آن ۸cm^۲ باشد.