جواب صفحه ۲۴ و ۲۵ هندسه یازدهم
در این نوشته با جواب صفحه ۲۴ و ۲۵ هندسه یازدهم همراه شما هستیم.
جواب صفحه ۲۴ و ۲۵ هندسه یازدهم
میدانیم برای اینکه دایرهای از دو نقطه بگذرد، باید مرکز آن روی عمود منصف پارهخطی باشد که آن دو نقطه دو سر آن است؛ بنابراین:
یک چند ضلعی، محاطی است اگر و فقط اگر عمود منصفهای همه ضلعهای آن در یک نقطه همرس باشند.
این نقطه مرکز دایره محیطی چند ضلعی است. چرا؟
فرض : چند ضلعی محاطی است . حکم : عمود منصف ها ی همه ی ضلع ها ی آن در یک نقطه همرسند.
باتوجه به تعریف چند ضلعی محاطی و فرض واضح است که فاصله ی همه رأس های چند ضلعی تا مرکز دایره به یک اندازه است (شعاع دایره) در نتیجه بنا برخاصیت عمود منصف فاصله مرکز دایره از دوسر هر ضلع به یک فاصله ( شعاع دایره ) است ، پس مرکز دایره روی عمود منصف این اضلاع قرار دارد.در نتیجه عمود منصف ها ی همه ی ضلع ها ی آن در یک نقطه( مرکز دایره ) همرسند.
فرض : عمود منصف ها ی همه ی ضلع ها ی چندضلعی در یک نقطه همرسند. حکم : چند ضلعی محاطی است .
باتوجه به فرض و خاصیت عمود منصف همه ی رأس های چند ضلعی از نقطه ی همرسی عمود منصف ها به یک فاصله اند و در نتیجه این نقاط بنا بر تعریف دایره ، روی دایره ای به شعاع این فاصله ی ثابت قرار داردند و بنا بر تعریف چند ضلعی محاطی این چند ضلعی محاطی است .
فعالیت
فرض کنید دایرهٔ C بر دو ضلع زاویهای مانند شکل مماس باشد.
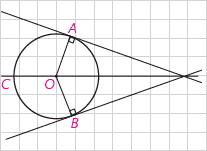
الف)
۱- پاره خطهایی که مرکز دایره را به نقاط تماس اضلاع با دایره وصل میکند، رسم کنید و آنها را OB و OA بنامید.
۲- پاره خطهای OA و OB برای دایره چه نوع پاره خطی هستند؟ شعاعهای دایرهاند.
۳- فاصلهٔ نقطهٔ O(مرکز دایره) تا ضلعهای زاویه مفروض با طول پاره خطهای رسم شده (OA و OB) چه رابطهای دارد؟ باهم برابرند. زیرا شعاع نقطه تماس برخط مماس عمود است.
۴- با توجه به (۲) و (۳) فاصله مرکز دایره از دو ضلع زاویه به یک فاصله است و بنابراین نقطه O روی نیمساز زاویه است.
۵- فرض کنید مانند شکل زیر، دایره در یک چند ضلعی محاط شده باشد. چرا مرکز دایره، محل برخورد نیمسازهای زاویههای داخلی چند ضلعی است؟
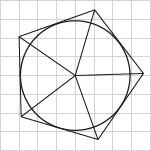
بنا به تعریف چند ضلعی محاطی، اضلاع چندضلعی بر دایره مماس هستند و میدانیم شعاع در نقطهٔ تماس برخط مماس عمود است، پس این شعاعها همان فاصلهی مرکز دایره از اضلاع چندضلعی هستند و همگی با هم برابرند. بنا برخاصیت نیمساز مرکز این دایره روی نیمساز هریک از زاویههای داخلی چند ضلعی است به عبارتی مرکز دایره محل برخورد نیمسازهای داخلی چندضلعی است.
ب) فرض کنید یک چند ضلعی مانند شکل زیر به گونهای باشد که نیمسازهای زوایای داخلی آن در نقطهٔ O یکدیگر را قطع کرده باشند و OH پاره خط عمود به یک ضلع چند ضلعی باشد. دایرهای به مرکز O و شعاع OH برای چند ضلعی مفروض چه نوع دایرهای است؟ چرا؟
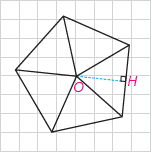
نقطهٔ O روی نیمساز زوایای داخلی است پس بنا بر خاصیت نیمسازها: OH=OH1=OH2=OH3=OH4
همچنین OH1 و OH2 و OH3 و OH4 همگی بر اضلاع عمود هستند. در نتیجه وقتی دایرهای به شعاع OH رسم میکنیم شعاعها بر اضلاع عمود هستند پس اضلاع بر دایره در نقطهٔ تماسشان عمودند یعنی دایره بر اضلاع چندضلعی مماس است در نتیجه بنا به تعریف دایره محاطی است.

برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
