جواب صفحه ۲۷ هندسه یازدهم
در این نوشته با جواب صفحه ۲۷ هندسه یازدهم همراه شما هستیم.
جواب صفحه ۲۷ هندسه یازدهم
۱- فرض کنیم چهار ضلعی ABCDمحاطی باشد؛ مجموع اندازههای C^,A^نصف مجموع اندازههای کمانهای DCB و DAB است؛ اما مجموع اندازههای این دو کمان ۱۸۰ درجه است و در نتیجه مجموع اندازههای C^,A^برابر ۱۸۰ درجه است.
به همین ترتیب D^,B^مکملاند.
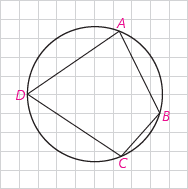
۲- فرض کنیم C^,A^ مکمل باشند. با برهان خلف ثابت میکنیم چهارضلعی ABCD محاطی است. از سه نقطه B، C و D همواره یک دایره میگذرد؛ چرا؟
زیرا عمودمنصفهای اضلاع یک مثلث همرسند و مرکز دایرهی محیطی هر چندضلعی نقطهٔ همرسی عمودمنصفهای اضلاع است.
اگر این دایره از A نگذرد، خط AD را در نقطهای دیگری مانند A′ قطع میکند که A′بین A و D یا A بین A′ و D است. اکنون چهارضلعی A′BCD محاطی است؛ پس C^ و BA′D^ مکملاند؛ در نتیجه باید Aˆ و BA′Dˆ هماندازه باشند و این ممکن نیست؛ چرا؟
زیرا در هر مثلث هر زاویه خارجی از زاویه داخلی غیر مجاورش بزرگتر است.
در نتیجه A′ همان A است.
برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
