جواب صفحه ۲۸ ریاضی یازدهم تجربی
در این نوشته با جواب صفحه ۲۸ ریاضی یازدهم تجربی همراه شما هستیم.
جواب صفحه ۲۸ ریاضی یازدهم تجربی
میخواهیم عمودمنصف پارهخط AB را رسم کنیم.
۱- دهانهٔ پرگار را بیش از نصف طول ABباز کنید و یک بار به مرکز نقطهٔ A و بار دیگر به همان شعاع و به مرکز B کمان بزنید تا دو کمان یکدیگر را در نقاطی مانند P و Q قطع کنند.
۲- آیا نقاط P و Q نقاطی متعلق به عمودمنصف AB هستند؟ چرا؟
بله فاصله ی این دو نقطه از دو سر پاره خط یکسان است (شعاع های دایره اند.) پس نتیجه می گریم که این نقاط روی عمود منصف AB قرار دارند.
۳- آیا با داشتن نقاط Pو Q میتوان عمودمنصف AB را مشخص کرد؟ چرا؟
بله اگر دو نقطه از خطی معلوم باشد می توان آن خط را مشخص کرد.
۴- حال عمودمنصف AB را رسم کنید.
خط PO همان عمود منصف پاره خط AB است .
رسم خط عمود بر یک خط، از نقطهای روی آن
خط d و نقطهٔ M روی آن مانند شکل مشخص شدهاند. میخواهیم خطی رسم کنیم که از M بگذرد و بر خط dعمود باشد.
۱- به کمک پرگار نقاطی مانند A و B بر خط d بیابید AM=MB باشد.
برای این منظور کافی است به مرکز M و شعاع دلخواه کمانی رسم کنیم طوری این کمان خط d را در دو نقطه قطع می کند. این دو نقطه را A و B می نامیم .
چون A و B روی دایره به مرکز M هستند پس M وسط آن ها است .
۲- عمودمنصف پارهخط AB را رسم کنید.
با استفاده از روش رسم عمود منصف که قبلا توضیح داده شده است رسم می کنیم.
۳- عمودمنصف پارهخط AB خطی است که بر خط d عمود است و از نقطهٔ M می گذرد .
رسم خط عمود بر یک خط، از نقطهای غیر واقع بر آن
خط d و نقطهٔ P مانند شکل داده شدهاند. میخواهیم خطی رسم کنیم که از نقطهٔ P بگذرد و بر خط d عمود باشد.
۱- به کمک پرگار نقاطی مانند A و B را برخط d بهگونهای بیابید که از نقطهٔ P به یک فاصله باشند.
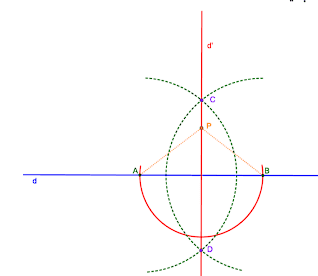
برای این کار دایره ای به مرکز P و شعاع بیش از فاصله ی نقطه P از خط d رسم می کنیم تا خط رادر دونقطه ی A و B قطع کند .
واضح است که فاصلهP که مرکز دایره است از A و B به یک اندازه است
۲- عمودمنصف پارهخط AB را رسم کنید.
عمود منصف AB را به روشی که قبلا توضیح داده شده رسم می کنیم.
۳- آیا عمودمنصف پارهخط AB از نقطهٔ P میگذرد؟ چرا؟
بله زیرا هر نقطه که روی عمود منصف AB باشد از دو سر این پاره خط به یک فاصله است و بالعکس و چون فاصله ی نقطه ی P از دو نقطه ی A و B به یک فاصله است پس P نیز روی عمود منصف AB قرار دارد.
عمودمنصف پارهخط AB برخط d عمود است و از نقطهٔ p می گذرد.
رسم خط موازی با خط داده شده از نقطهای غیر واقع بر آن
خط d و نقطهٔ P مانند شکل مقابل داده شدهاند. میخواهیم خطی رسم کنیم که از نقطهٔ P بگذرد و با خط d موازی باشد.
۱- خط d1 را بهگونهای رسم کنید که از نقطهٔ P بگذرد و بر خط d عمود باشد.
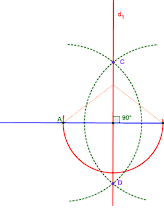
به روش رسم خط عمود بری یک خط از نقطه ی خارج آن از نقطه ی P خط d را عمود بر خط d رسم می کنیم.
۲- خط d2 را بهگونهای رسم کنید که از نقطهٔ P بگذرد و بر خط d1 عمود باشد.
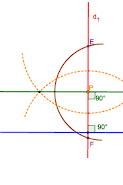
به روش رسم خطی عمود بریک خط را نقطه ای روی خط ۲ d را عمود برخط d1 رسم می کنیم .
۳- خط d2 نسبت به خط d چه وضعیتی دارد؟ چرا؟ (خط d1 را مورب درنظر بگیرید)
خط ۲d موازی خط d است . دو خط عمود بر یک خط باهم موازی هستند.
برخی خواص نیمساز و ترسیم آن
۱- در شکل زیر نیمخط Ow نیمساز زاویهٔ vOu است. فرض کنید P یک نقطهٔ دلخواه روی Ow باشد. ثابت کنید فاصلهٔ نقطهٔ P از دو ضلع زاویهٔ vOuیکسان است. (یعنی اگر از نقطهٔ P عمودهایی بر Ov و Ou رسم کنیم، طول آنها باهم برابر است.)

۲- در شکل زیر فاصلهٔ نقطهٔ P از دو ضلع زاویهٔ vOu یکسان است. نشان دهید که نقطهٔ P روی نیمساز زاویه قرار دارد.
(راهنمایی: پارهخط OP را و دو عمود از نقطهٔ P بر Ou و Ov رسم کنید و با استفاده از همنهشتی مثلثها نشان دهید OP همان نیمساز زاویهٔ uOv است.)

۳- رسم نیمساز یک زاویه
الف) زاویهٔ uOv را درنظر بگیرید. به مرکز O و به شعاع دلخواه کمانی رسم کنید تا نیمخطهای Ou و Ov را در نقاطی مانند P و Q قطع کند.
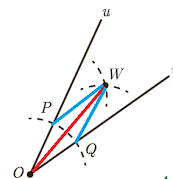
– طول پارهخطهای OP و OQ نسب به هم چگونهاند؟
با هم برابرند زیرا شعاع های دایره هستند.
ب) دهانهٔ پرگار را کمی بیش از نصف طول پارهخط PQ باز کنید و یک بار به مرکز P و بار دیگر به مرکز Q کمانی رسم کنید تا دو کمان مانند شکل یکدیگر را در نقطهای مانند W قطع کنند. طول پارهخطهای PW و QW نسبت به هم چگونهاند؟
باهم برابرند زیرا شعاع های دایره اند
پ) پارهخطهای PO، WO و WQرا رسم کنید. دو مثلث OPW و OQW نسبت به هم چگونهاند؟ چرا؟
باهم همنهشت هستند به حالت ( ض ض ض )
– اندازهٔ زاویههای POW و QOW نسبت به هم چگونهاند؟ چرا؟
این دو زاویه بنا بر اجزای متناظر باهم برابر می شوند.
برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
