جواب صفحه ۲۸ هندسه یازدهم
در این نوشته با جواب صفحه ۲۸ هندسه یازدهم همراه شما هستیم.
جواب صفحه ۲۸ هندسه یازدهم
۲- فرض کنید: AB+CD=BC+AD
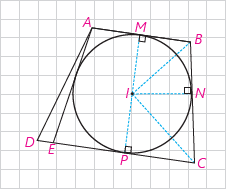
نیمسازهای دو زاویهٔ B و C همدیگر را در نقطهای مانند I قطع میکنند. با توجه به ویژگی نیمساز، چرا نقطهٔ I از سه ضلع CD و BC و AB به یک فاصله است؟ (IM=IN=IP)
نقطهٔ I روی نیمساز زاویهٔ B است پس IM=IN (۱)
نقطهٔ I روی نیمساز زاویهٔ C است پس IP=IN(2)
از (۱) و (۲) نتیجه میگیریم که: IP=IN=IM پس نقطهٔ I از سه ضلع CD، BC و AB به یک فاصله است.
چرا دایرهای به مرکز I و شعاع IM بر AB و BCو CD مماس است؟
زیرا این شعاعها در نقاط اشتراک با دایره بر آن عمود هستند.
حال اگر این دایره بر AD هم مماس باشد، حکم ثابت شده است.
اما اگر این دایره بر AD مماس نباشد از A بر آن مماسی رسم میکنیم تا خط CD را در نقطهای مانند E قطع کند؛ در این صورت E بین P و D یا D بین E و P واقع میشود. پس، AB+EC=AE+BC؛ (چرا؟)
چهار ضلعی ABCE محیطی است پس بنا بر بند (۱) همین قضیه نتیجه میگیریم: AB+CE=AE+BC
از این رابطه با استفاده از رابطه فرض چگونه نتیجه میگیرید: AD=DE+AE؟
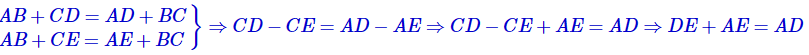
این رابطه امکان ندارد؛ (چرا؟)
بنا بر نامساوی مثلثی در مثلث ADE داریم: DE+AE>AD پس رابطهی فوق امکان ندارد؛ مگر این که E همان D یاشد.
کار در کلاس
جدول زیر را کامل کنید.
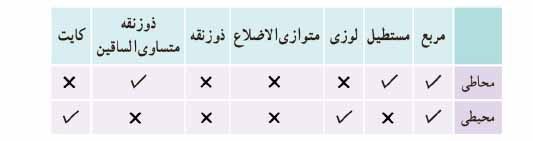
برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
