جواب صفحه ۵۱ ریاضی نهم

در این نوشته با جواب صفحه ۵۱ ریاضی نهم همراه شما هستیم.

جواب صفحه ۵۱ ریاضی نهم

کار در کلاس

در شکل مقابل می‌دانیم AB=CD،

۱- چرا AB⌢=CD⌢؟ وترهای مساوی از یک دایره، کمان‌های مساوی ایجاد می‌کنند.
۲- جاهای خالی را با عبارت‌های مناسب پر کنید:

کمان‌های مساوی در یک دایره، وترهای مساوی ایجاد می‌کنند. چون ABC⌢=DCB⌢، پس وترهای متناظر آنها نیز با هم مساوی‌اند. AC=BD

تمرین

١- در شکل مقابل ABCD متوازی الاضلاع است و M و N و P  و Q وسط‌های اضلاع متوازی الاضلاع‌اند، ثابت کنید: MN=PQ

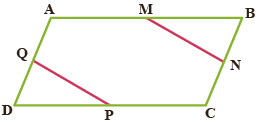
در متوازی الاضلاع ضلع‌های روبرو با هم موازی‌اند. قبلاً ثابت کردیم که ضلع‌های روبرو با هم مساوی و زاویه‌های روبرو هم با یکدیگر مساوی هستند. پس داریم؛

در نتیجه اجزای متناظر دو مثلث همنهشت با هم برابرند. پس MN=PQ

۲- در شکل مقابل O مرکز دایره است و BC و AD بر دایره مماس‌اند، نشان دهید که AD و BC برابرند.

۳- در شکل مقابل، مثلث ABC متساوی الساقین است و M و N روی قاعدهٔ BC طوری قرار دارند که BM=NC.
نشان دهید مثلث AMIN هم متساوی الساقین است.

چون مثلث ABC متساوی‌الساقین است، پس AB=AC و همچنین B∧=C∧ با توجه به فرض مساله هم BM=NC. پس به حالت (ض ز ض) در دو مثلث ANC و AMB داریم؛

در نتیجه اجزای متناظر دو مثلث همنهشت با هم برابرند. پس AM=AN و در نتیجه مثلث AMN نیز متساوی‌الساقین است.

۴- در مستطیل ABCD، پاره‌خط‌های BE و AF طوری رسم شده که دو زاویهٔ A1 و B1 برابرند. ثابت کنید BE و AF مساوی‌اند.

در مستطیل اضلاع روبرو با هم مساوی‌اند، پس AD=BC و همچنین همه زاویه‌ها برابر ۹۰ درجه هستند، پس A∧=B∧=۹۰. با توجه به فرض مساله هم A∧۱=B∧۱. بنابراین داریم؛

۵- نشان دهید در هر مثلث متساوی الساقین، فاصلهٔ هر نقطهٔ دلخواه روی نیمساز زاویهٔ رأس از دو سر قاعده، برابر است: MB=MC.
به حالت (ض ز ض) در دو مثلث ABM و ACM داریم؛