جواب فعالیت صفحه ۳۲ و ۳۳ هندسه یازدهم
در این نوشته با جواب فعالیت صفحه ۳۲ و ۳۳ هندسه یازدهم همراه شما هستیم.
جواب فعالیت صفحه ۳۲ و ۳۳ هندسه یازدهم
۱- به تصویر زیر دقت کنید.
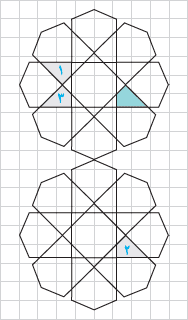
اگر چهارضلعیهای ۱، ۲ و ۳ را تبدیل یافتهٔ چهارضلعی رنگ شده بدانیم:
الف) کدام چهار ضلعی، انتقال یافتهٔ چهارضلعی رنگ شده است؟ چهار ضلعی ۲ انتقال یافتهٔ چهارضلعی رنگ شده است.
ب) کدام چهارضلعی بازتاب چهارضلعی رنگ شده است؟ چهار ضلعی ۳ بازتاب چهارضلعی رنگ شده است.
پ) کدام شکل، دوران یافتهٔ شکل رنگ شده است؟ چهار ضلعی ۱ دوران یافتهٔ چهارضلعی رنگ شده است.
۲- الف) بازتاب شکل زیر را نسبت به خط d رسم کنید.
(توضیح دهید که چگونه این کار را انجام میدهید. در این حالت خط d نسبت به پارهخطی که هر نقطه را به تصویرش نظیر میکند، چه وضعیتی دارد؟)
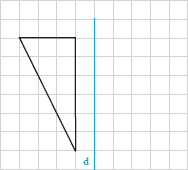
از هر رأس مثلث بر خط d عمودی رسم میکنیم و سپس به اندازهی آن پارهخط امتداد میدهیم تا تصویرش بهدست آید. (AM=A′M,BN=B′N,CM=C′M) سپس نقاط تصویر یعنی A′، B′ و C′ را به هم وصل میکنیم. مثلث A′B′C′ بازتاب مثلث ABC است.
خط d عمودمنصف پارهخطی است که هر نقطه را به تصویرش وصل میکند.
ب) آیا این تبدیل، موقعیت شکل اولیه را تغییر میدهد؟ اندازهها را چطور؟
موقعیت شکل را تغییر میدهد اما اندازهها را تغییر نمیدهد.
پ) آیا در این تبدیل، شیب هر پارهخط با شیب پارهخط متناظر در تصویر آن برابر است؟
خیر شیب پارهخط BC با شیب پارهخط متناظرش B′C′ برابر نیست.
ت) آیا حالتی وجود دارد که بازتاب، شیبخط را حفظ کند؟
اگر خط مورد نظر موازی یا عمود بر محور بازتاب باشد آنگاه شیب آن حفظ میشود.
در شکل بالا همانطور که میبینیم پارهخط AC بخشی از خط عمود بر خط d است و تصویر آن نیز روی همان خط عمود قرار خواهد گرفت و به همین دلیل شیب پارهخط A′C′ با شیب پارهخط AC برابر است.
اگر خط مورد نظر موازی محور بازتاب باشد تصویرش هم با آن موازی است پس هم شیب خواهند شد.
۳- الف) تصویر شکل زیر را تحت انتقال با بردار v رسم کنید (توضیح دهید که چگونه این کار انجام میدهید).
با توجه به بردار v باید رأسهای مربع را ۵ واحد به سمت راست و ۳ واحد به سمت پایین انتقال بدهیم تا نقاط تصویر بهدست آیند. واضح است که باتوجه به شکل بردارهایی که هر نقطه را به تصویرش برده است با بردار v برابر هستند. سپس نقاط تصویر را به ترتیب به هم وصل میکنیم. مربع A′B′C′D′انتقال یافتهی مربع ABCD تحت بردار v است.
در این حالت پارهخط هایی که هر نقطه را به تصویرش نظیر میکنند، نسبت به هم چه وضعیتی دارند؟
پاره خطهایی که هر نقطه را به تصویرش نظیر میکنند باهم موازی هستند.
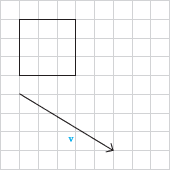
ب) آیا این تبدیل، موقعیت شکل اولیه را حفظ میکند؟ اندازهها را چطور؟ این تبدیل موقعیت شکل اولیه را حفظ نمیکند ولی اندازهها را حفظ میکند.
پ) آیا در این تبدیل، شیب هر پارهخط با شیب پارهخط متناظر در تصویر آن برابر است؟ در این تبدیل، شیب هر پاره خط با شیب پاره خط متناظر در تصویرش برابر است.
ت) آیا با انجام این تبدیل اندازه زاویهها ثابت میماند؟ در این تبدیل زاویه بین خطوط در شکل و تصویر متناظر آن حفظ میشود.
۴- در سال های گذشته دیدید که برای دوران دادن هر شکل به مرکز دوران O و به اندازهٔ زاویهٔ α، کافی است هر نقطه از شکل، مثل نقطهٔ A را به مرکز دوران یعنی O وصل کنیم؛ سپس در جهت خواسته شده به کمک OAزاویهای برابر α رسم، و روی ضلع دیگر این زاویه پارهخطی به اندازهٔ OA جدا کنیم تا نقطهٔ A′بهدست آید.
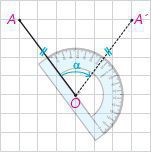
میخواهیم مثلث ABC را حول مرکز O، ۹۰ درجه در جهت حرکت عقربههای ساعت دوران دهیم؛ به ترتیبی که گفته شد نقاط Aو B را دوران دادهایم.
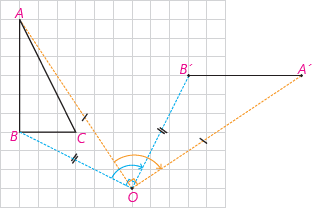
الف) به همین ترتیب تصویر نقطهٔ C را پیدا، و شکل را کامل کنید.
ب) آیا این تبدیل، موقعیت شکل اولیه را حفظ میکند؟ اندازهها را چطور؟ این تبدیل موقعیت شکل اولیه را حفظ نمیکند ولی اندازهها را حفظ میکند.
پ) آیا در این تبدیل، همواره شیب پارهخط اولیه با شیب پارهخط تصویر آن برابر است؟ در این تبدیل شیب پارهخط اولیه با شیب پارهخط تصویر آن برابر نیست.
ت) آیا میتوانید زاویهٔ دوران را طوری تعیین کنید که دوران تحت آن، شیبخط را حفظ کند؟ اگر زاویهٔ ۰، ۱۸۰ و یا ۳۶۰ درجه انتخاب شود دوران تحت آن، شیبخط را حفظ میکند.
برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
