جواب فعالیت صفحه ۲۱ هندسه یازدهم

در این نوشته با جواب فعالیت صفحه ۲۱ هندسه یازدهم همراه شما هستیم.

حل صفحه ۲۱ هندسه یازدهم

فرض کنیم مانند شکل خط m در نقاط و T بر دو دایره مماس است و شعاع های OTو ‘O’T رسم شده است. فرض کنیم فاصله بین مرکزهای دو دایره برابر d باشد؛ از خطی موازی خط m رسم میکنیم تا شعاع OT را در نقطه ای مانند H قطع کند.

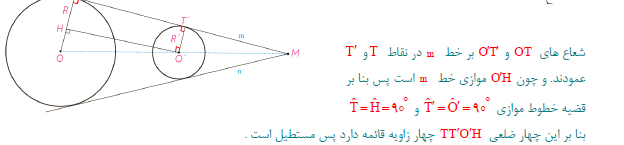
ب) با توجه به قضیه فیثاغورس در مثلث OHO، تساوی زیر را توجیه کنید.

ب با توجه به کار در کلاس قبل بگویید چرا اگر دو مماس مشترک m و n منقاطع باشند، نقطه تقاطع آنها روی خط OO خواهد بود؟

فرض کنیم این دو مماس مشرک در نقطه ی M یکدیگر را قطع کنند با توجه به بند (ب) کار در کلاس قبل OM نیمساز زاویه M است . همچنین OM هم نیمساز زاویه M است و چون هر زاویه یک نیمساز دارد در نتیجه OM و OM بر هم منطبق هستند در نتیجه نقطه تقاطع مماسها روی خط OO قرار دارد.

ت)به مرکز و به شعاع RR دایره ای رسم کنید. پاره خط OH برای دایره رسم شده چگونه خطی است؟

پاره خط OH بر این دایره مماس است .

ث) فرض کنید در دایره داده شده و رسم مماس مشترک خواسته شده باشد. از آنجا که مرکزها و شعاع های دو دایره معلوم است، می توان دایرۀ مطرح شده در قسمت (ت) را رسم کرد و سپس مماس OH را بر آن رسم کرد؛ در این صورت چگونه می توانید مماس TT را رسم کنید؟

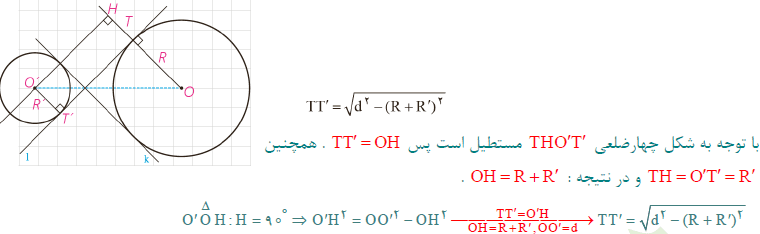
۲-دو مماس مشترک ۱ و K نیز بر دو دایره متخارج مطابق شکل رسم شده است مرکزهای دو دایره در دو طرف مماس مشترکاند با به کار بردن قضیه فیثاغورس در 0OH مانند قبلی نشان دهید :

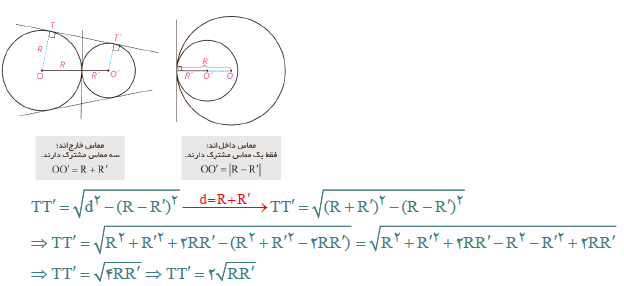
۳- دو دایره مماس دو دایره را که فقط یک نقطه مشترک داشته باشند مماس می نامند. در این نقطه مشترک یک خط بر هر دو مماس است. اگر مرکزهای دو دایره در دو طرف این مماس باشند آن دو ،دایره مماس برونی است و اگر هر دو مرکز در یک طرف این مماس باشند، آنها را مماس درونی می نامند.