جواب فعالیت صفحه ۳۶ هندسه یازدهم
در این نوشته با جواب فعالیت صفحه ۳۶ هندسه یازدهم همراه شما هستیم.
جواب فعالیت صفحه ۳۶ هندسه یازدهم
میخواهیم با استدلال دقیقتری نشان دهیم بازتاب، تبدیلی طولپا است. حالتهای مختلف یک پارهخط را نسبت به خط بازتاب d در نظر میگیریم و در حالت نشان میدهیم که اندازهٔ پارهخط با اندازهٔ تصویر آن برابر است.
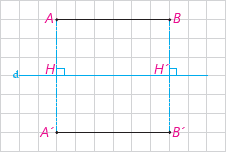
الف) ابتدا مسئله را برای حالتی در نظر میگیریم که AB با خط d موازی است. بازتاب A و B را نسبت به خط d پیدا میکنیم و آن را A′ و B′ مینامیم.
چهار ضلعی ABA′B′چهارضلعی است؟ چرا؟
طول پارهخطهای AB و A′B′ نسبت به هم چگونهاند؟

ب) حال فرض میکنیم که فقط یکی از نقاط انتهایی پارهخط داده شده روی خط بازتاب باشد.
(اگر هر دو نقطهٔ ابتدا و انتهای پارهخط داده شده روی خط بازتاب باشد، اثبات بدیهی است؛ چرا؟)
خوب در این حالت بازتاب پارهخط MA بر روی خط و بر روی خط و بر روی خودش منطبق است.
S(M)=M,S(A)=A⇒MA=MA
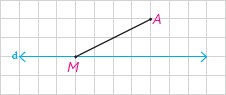
بازتاب A نسبت به خط d، نقطهٔ A′ و بازتاب M، خود M است.
به عبارتی: S(A)=A′ و S(M)=M
آیا میتوانید به کمک هم نهشتی مثلثها، دلیلی برای تساوی MA=MA′ ارائه کنید؟
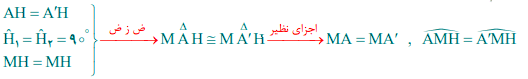
آیا میتوانید این تساوی را به روش دیگری نشان دهید؟ (از خاصیت عمود منصف یک پارهخط کمک بگیرید.)
MA=MA′
پ) در حالتی که پارهخط AB با خط بازتاب d، نه موازی و نه متقاطع باشد، پارهخط AB را امتداد میدهیم تا خط بازتاب را در نقطهٔ M قطع کند.
نقطه B′بازتاب نقطه B را نسبت به خط بازتاب پیدا، و پارهخط MB′ را رسم میکنیم. ادعا میکنیم که تصویر نقطه A نیز روی خط MB′واقع میشود؛ چرا؟
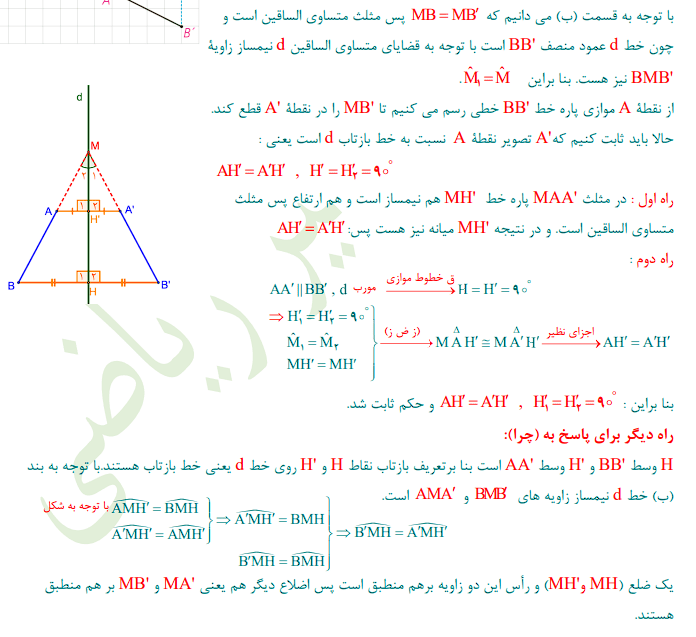
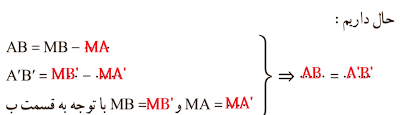
ت) در حالتی که پارهخط AB خط بازتاب را در نقطهای مثل M قطع کند، بازتاب نقطه A را نسبت به خط d پیدا میکنیم و آن را نقطه A′ مینامیم.
پارهخط MA′ را رسم میکنیم و امتداد میدهیم و ادعا میکنیم که بازتاب نقطه Bیعنی نقطه B′ هم بر امتداد MA′واقع است؛ چرا؟

برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
