جواب تمرین صفحه ۲۹ تا ۳۱ هندسه یازدهم

در این نوشته با جواب تمرین صفحه 29 تا 31 هندسه یازدهم همراه شما هستیم.

جواب تمرین صفحه 29 تا 31 هندسه یازدهم

1- ثابت کنید یک ذوزنقه، محاطی است، اگر و تنها اگر متساوی‌الساقین باشد.

2- مساحت مثلث متساوی‌الاضلاعی را به‌دست آورید که در دایره‌ای به شعاع Rمحاط شده باشد.

3- ثابت کنید عمود منصف یک ضلع هر مثلث و نیمساز زاویهٔ مقابل به آن ضلع، یکدیگر را روی دایرهٔ محیطی مثلث قطع می‌کنند.

4- یک ذوزنقه، هم محیطی است و هم محاطی. ثابت کنید مساحت این ذوزنقه برابر است با میانگین حسابی دو قاعده آن ضرب در میانگین هندسی آنها.

5- اگر rb,ra و rc شعاع‌های سه دایره محاطی خارجی مثلث و r شعاع دایره محاطی داخلی باشد، نشان دهید.

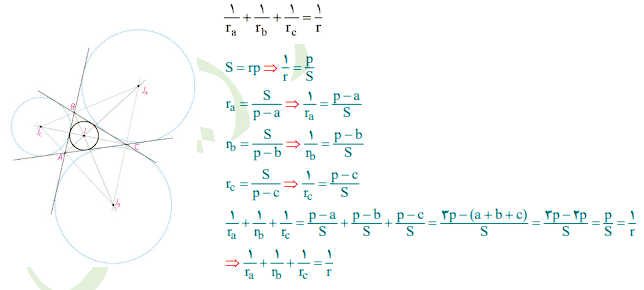
به همین ترتیب اگر ha، hbو hc اندازه‌های سه ارتفاع باشند، نشان دهید:

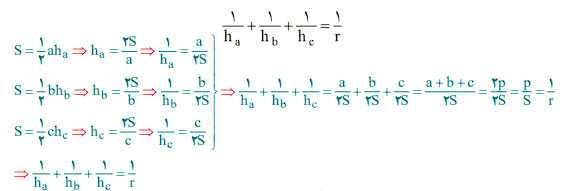
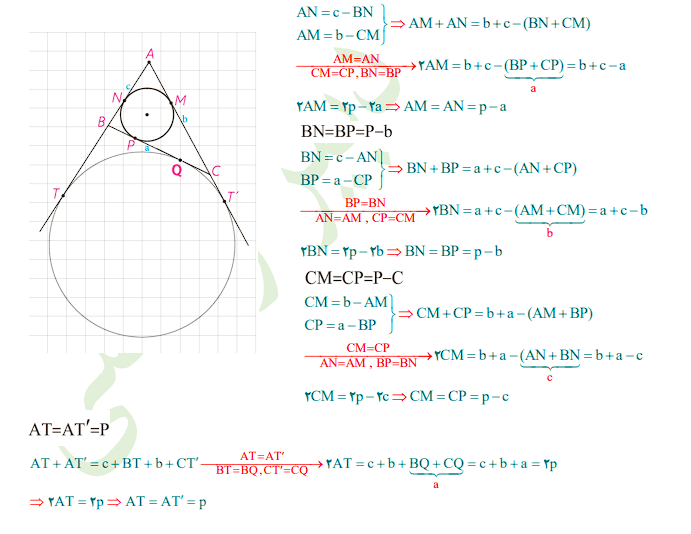
6- اگر نقاط تماس دایره محاطی داخلی مثلث ABC با اضلاع آن M، N و K باشند و T و T′ نقطه‌های تماس یک دایره محاطی خارجی با خط‌های شامل دو ضلع باشند، نشان دهید:

8- شش ضلعی منتظم ABCDEF مفروض است با امتداد دادن اضلاع شش ضلعی. مطابق شکل، مثلث MNP را ساخته‌ایم

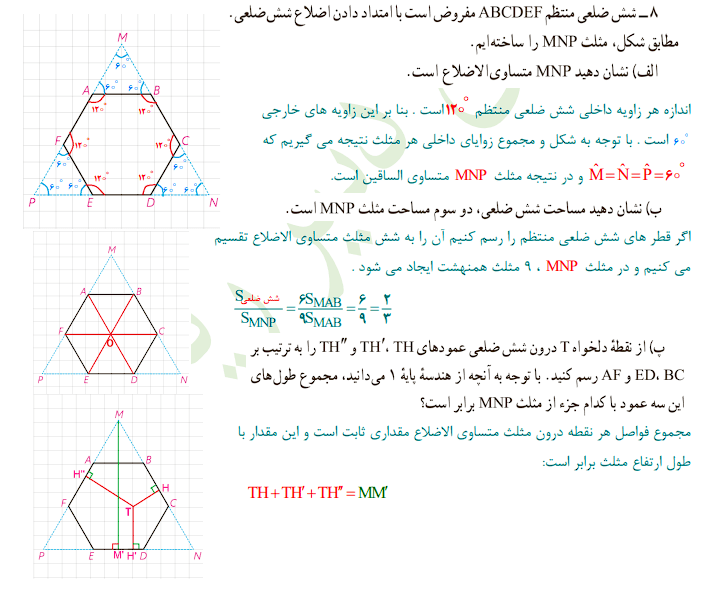
ت) مجموع مساحت‌های مثلث‌های TBC، TDE و TAF چه کسری از مساحت مثلث MNP است؟ نشان دهید:

9- دو قطر عمود بر هم AC و BD از یک دایره را رسم می‌کنیم؛ چهارضلعی ABCD یک مربع است؛ چرا؟ عمود منصف‌های ضلع‌های این مربع را رسم کنید تا دایره را قطع کنند. نشان دهید هشت ضلعی AMBQCPDN منظم است.