جواب فعالیت صفحه ۳۹ ریاضی نهم

در این نوشته با جواب فعالیت صفحه ۳۹ ریاضی نهم همراه شما هستیم.

جواب فعالیت صفحه ۳۹ ریاضی نهم

۱- در مسئلهٔ زیر، فرض و حکم را بنویسید و اشکال استدلال داده شده را بیابید، سپس استدلال درستی برای آن بنویسید.

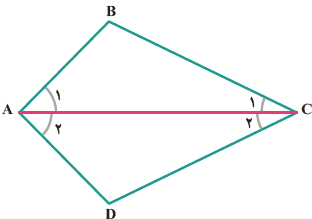
مسئله: در شکل مقابل پار خط AC نیمساز زاویهٔ A است و اضلاع AB و AD برابرند. ثابت کنید مثلث‌های مثلث ABC△ و ADC△ هم نهشت‌اند.

BD=DC :حکم
AB=AC,Aˆ۱=Aˆ۲ :فرض

استدلال: چون AC نیمساز است، داریم و از طرفی AC نیز ضلع مشترک در هر دو مثلث است، لذا دو مثلث ABC و ADC به حالت دو زاویه و ضلع بین (ز ض ز) هم نهشت‌اند.

۲- مثلث زیر متساوی الساقین و AD نیمساز وارد بر قاعدهٔ آن است. با استدلال زیر نشان داده‌ایم که نیمساز وارد بر قاعده، میانه نیز می‌باشد.

لذا نقطهٔ D وسط BC است و AD میانه است.
آیا در مثلث ABC می‌توان نتیجه گرفت که نیمساز زاویهٔ B نیز میانهٔ ضلع مقابل آن است؟ به عبارتی، آیا می‌توان خاصیت اثبات شده برای نیمساز A را به نیمساز دیگر تعمیم داد؟

استدلال: چون AD نیمساز زاویه A است، پس: Aˆ۱+Aˆ۲ و چون مثلث ABCΔ متساوی الساقین است، پس AB=AC و ضلع AD در دو مثلث مشترک است، پس مثلث‌های ADB و ADC به حالت دو ضلع و زاویۀ بین (ض‌زض) با هم همنهشتند، پس اجزای متناظر آنها برابر است. درنتیجه: BD=DC

نیمساز زاویه B میانۀ ضلع مقابل نیست. زیرا وقتی این نیمساز رسم می‌شود، دیگر اضلاع مساوی مثلث متساوی‌الساقین در دو مثلث حاصل کمکی به همنهشتی مثلث‌ها نمی‌کنند.

۳- با استدلال زیر به سادگی می‌توان نتیجه گیری کرد که قطر AC از مربع ABCD نیمساز زاویه‌های A و C است. چون دو مثلث ABC و ADC به حالت سه ضلع هم نهشت‌اند و زوایای متناظر با هم برابر‌ند؛ بنابراین Aˆ۱=Aˆ۲ و Cˆ۱=Cˆ۲ و لذا AC نیمساز است.

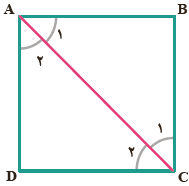
آیا می‌توان با استدلالی مشابه، این خاصیت را به قطر دیگر نیز تعمیم داد و گفت به طور کلی در مربع هر قطر نیمساز زاویه‌های دو سر آن قطر است؟

بله. دقیقاً مشابه همین استدلال را می‌توان برای همنهشتی دو مثلث ABD و BDC استفاده کرد.

۴- به نظر شما چرا در فعالیت ۲ خاصیت موردنظر قابل تعمیم به نیمسازهای دیگر نبود؛ اما در فعالیت ۳ خاصیت موردنظر به قطر دیگر تعمیم داده می‌شود؟

در فعالیت ۱، یکی از فرض های مساله در مورد نیمسازهای دیگر قابلیت استفاده نداشت (برابری دو ساق مثلث). اما در فعالیت ۲، عین ویژگی‌هایی که برای یک قطر وجود دارد، برای قطر دیگر هم وجود دارد و استفاده می‌شود.

وقتی خاصیتی را برای یک عضو از یک مجموعه ثابت کردیم، اگر تمام ویژگی‌هایی که در استدلال خود به کار برده‌ایم، در سایر عضوهای آن مجموعه نیز باشد، می‌توان درستی نتیجه را به همهٔ عضوهای آن مجموعه تعمیم داد.

نکته

۵- نقطه‌ای مانند P، روی عمودمنصف پاره خط AB در نظر می‌گیریم و به دو سر پاره خط وصل می‌کنیم. چون دو مثلث AHP و BHP به حالت (ض ز ض) هم نهشت‌اند، نتیجه می‌گیریم پاره خط‌های PA  و PB با هم برابر است

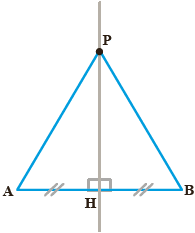
بنابراین فاصلهٔ نقطهٔ P، که روی عمودمنصف پاره خط AB است، از دو سر پاره خط AB یکسان‌اند.

آیا این اثبات برای اینکه نتیجه بگیریم نتیجهٔ بالا برای «هر» نقطهٔ روی عمودمنصف برقرار است، کافی است؟

برای هر نقطۀ دیگری روی عمود منصف، تمام ویژگی‌های استدلال فوق برقرار است. بنابراین هر نقطه روی عمودمنصف از دو سر پاره خط AB به یک فاصله است.