جواب کار در کلاس صفحه ۴۰ ریاضی نهم

در این نوشته با جواب کار در کلاس صفحه ۴۰ ریاضی نهم همراه شما هستیم.

جواب کار در کلاس صفحه ۴۰ ریاضی نهم

به استدلال‌هایی دقت کنید که چهار دانش آموز برای مسئلهٔ زیر آورده‌اند:
مسئله: مجموع زاویه‌های داخلی مثلث است.
استدلال حامد: حامد گفت یک مثلث متساوی الاضلاع را درنظر می‌گیریم؛ چون سه زاویه دارد و هر زاویه است، مجموع زاویه‌های مثلث است.

استدلال حسین: حسین چند مثلث مختلف با حالت‌های گوناگون کشید و زوایای آنها را اندازه گرفت و دید که در همهٔ آنها مجموع زوایای داخلی برابر است و نتیجه گرفت که مجموع زوایای داخلی هر مثلث است.

استدلال مهدی: مهدی شکل روبرو را، که از مثلث‌های هم نهشت تشکیل شده است کشید و با مشخص کردن زاویه‌های مثلث ABC مانند شکل استدلالی با استفاده از شکل به صورت زیر آورد:

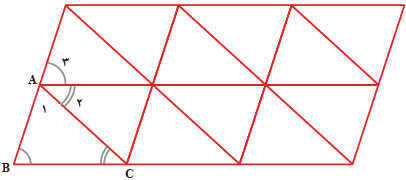
استدلال رضا: رضا گفت می‌دانیم که «هر خطی که دو خط موازی را قطع کند، با آنها هشت زاویه می‌سازد که مانند شکل چهار به چهار با هم مساوی‌اند».

دربارهٔ معتبر بودن استدلال‌های این دانش آموزان بحث کنید.

استدلال حامد: این استدلال فقط در مورد مثلث‌های متساوی الاضلاع درست است. آن هم در صورتی که فرض ۶۰ درجه بودن هر زاویه در یک مثلث متساوی‌الاضلاع را قبول داشته باشیم. بنابراین استدلال مناسبی نیست.

استدلال حسین: او زاویه‌های چند مثلث را اندازه‌گیری و مجموع زاویه‌ها را در هر مثلث حساب کرده است. با این حال ممکن است مثلثی وجود داشته باشد که مجموع زوایای آن ۱۸۰ درجه نباشد. او با اندازه‌گیری چند مثلث نمی‌تواند نتیجه خود را به هر مثلثی تعمیم دهد.

استدلال مهدی: اگر چه این استدلال روش جالبی به نظر می‌رسد اما مشخص نیست در این استدلال چگونه از کنار هم قرار گرفتن سه زاویۀ متفاوت مثلث‌های همنهشت، یک خط راست یا زاویۀ نیم‌صفحه حاصل شده است.

استدلال رضا: رضا از فرض‌هایی استفاده کرده است که درستی آنها قطعی است. این استدلال از این نظر که مجموع سه زاویه مثلث را به مجموع سه جزء از یک زاویه نیم صفحه تبدیل کرده است با استدلال مهدی شباهت دارد. ولی در استدلال رضا از همان ابتدا روشن است که Ad خطی موازی با BC است و بنابراین در نیم‌صفحه بودن آن هیچ شکی وجود ندارد. همچنین رضا با یک استدلال منطقی که مبتنی بر معلومات است، نشان داده است که مجموع زوایای داخلی مثلث برابر ۱۸۰ درجه است. دقت کنید که استلال او به مثلث خاصی اختصاص ندارد و به هر مثلثی قابل تعمیم است.