جواب صفحه ۹ ریاضی هشتم ⭐️ فعالیت و تمرین

در این نوشته با جواب صفحه ۹ ریاضی هشتم همراه شما هستیم.

جواب فعالیت صفحه ۹ ریاضی هشتم

۱- چگونه می‌توانیم به کمک بردارهایی که در شکل نمایش داده شده‌اند، درستی تساوی‌ها را نتیجه بگیریم؟ توضیح دهید.

$+۲\div 3=\frac{+2}{3}=+\frac{2}{3}$

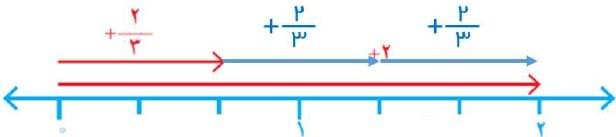
$-۳\div 4=\frac{-3}{4}=-\frac{3}{4}$

۲- مانند نمونه، کسر مساوی هر کسر را بنویسید.

$\frac{-2}{3}=-2\div 3=-(2\div 3)=-\frac{2}{3}$

$-\frac{3}{5}$$\frac{3}{-5}=$

$+\frac{4}{7}$$-\frac{-4}{7}=$

$+\frac{3}{4}$$\frac{-3}{-4}=$

جواب تمرین صفحه ۹ ریاضی هشتم

۱- آیا می‌توان گفت هر عدد صحیح و هر عدد طبیعی نیز عدد گویاست؟ چرا؟

پاسخ کوتاه: بله. زیرا هر عدد طبیعی و عدد صحیح را می‌توان به صورت کسر علامت‌دار نوشت.

تعریف عدد گویا

عدد گویا (Rational Number) عددی است که می‌تواند به صورت کسری از دو عدد صحیح نوشته شود، به طوری که مخرج کسر (عدد پایین) صفر نباشد. به عبارت دیگر، یک عدد گویا به صورت (\frac{a}{b}) است که در آن (a) و (b) هر دو عدد صحیح هستند

عدد صحیح و عدد طبیعی

1. عدد صحیح: اعداد صحیح شامل تمام اعداد مثبت، منفی و صفر هستند، مثل (-۳), (-۲), (-۱), (۰), (۱), (۲), (۳) و غیره.
2. عدد طبیعی: اعداد طبیعی شامل اعداد مثبت از ۱ به بالا هستند، مثل (۱), (۲), (۳) و غیره.

آیا هر عدد صحیح عدد گویا است؟

بله، هر عدد صحیح عدد گویا است. برای دیدن این موضوع، کافی است هر عدد صحیح را به صورت کسر بنویسیم. هر عدد صحیح (n) را می‌توان به صورت (\frac{n}{1}) نوشت. چون (۱) یک عدد صحیح و غیر صفر است، پس هر عدد صحیح به فرم (\frac{n}{1}) یک عدد گویا است.

مثلاً:

• عدد صحیح (۵) را می‌توان به صورت (\frac{5}{1}) نوشت که یک عدد گویا است.
• عدد صحیح (-۳) را می‌توان به صورت (\frac{-3}{1}) نوشت که نیز یک عدد گویا است.

آیا هر عدد طبیعی عدد گویا است؟

بله، هر عدد طبیعی نیز عدد گویا است. هر عدد طبیعی (n) را می‌توان به صورت (\frac{n}{1}) نوشت. چون (۱) یک عدد صحیح و غیر صفر است، پس هر عدد طبیعی به فرم (\frac{n}{1}) یک عدد گویا است.

مثلاً:

• عدد طبیعی (۴) را می‌توان به صورت (\frac{4}{1}) نوشت که یک عدد گویا است.
• عدد طبیعی (۷) را می‌توان به صورت (\frac{7}{1}) نوشت که نیز یک عدد گویا است.

۲- هریک از کسرهای سطر اول را به کسر مساوی‌اش در سطر دوم وصل کنید.

$\frac{3}{4}$ <===> $\frac{-3}{-4}$

$-\frac{3}{4}$ <===> $-\frac{-3}{-4}$

$\frac{3}{5}$ <===> $\frac{-3}{-5}$

$-\frac{3}{5}$ <===> $\frac{-3}{5}$

۳- جدول زیر را مانند نمونه کامل کنید.

نوع	عدد	$-(-(+۴))$	$-\frac{6}{2}$	$\sqrt{9}$	$-۲/۳$	۰	$\frac{3}{5}$	$-\frac{-8}{-3}$	$\frac{-4}{-2}$	$\frac{-1}{{{5}^{3}}}$	$\frac{12}{-4}$
طبیعی		*	×	*	×	×	×	×	*	×	×
صحیح		*	*	*	×	*	×	×	*	×	*
گویا		*	*	*	*	*	*	*	*	*	*

۴- ابتدا علامت هر عبارت را تعیین، و سپس آن را ساده کنید.

$+\frac{3}{4} = \frac{-8 \times (-18)}{12 \times 16}$

$\frac{3}{4} = \frac{8 \times 18}{12 \times 16}$

$-\frac{4}{35} = \frac{10 \times (-2)}{-7 \times 25}$