جواب فعالیت صفحه ۴۳ ریاضی هشتم
در این نوشته با جواب فعالیت صفحه ۴۳ ریاضی هشتم همراه شما هستیم.
جواب فعالیت صفحه ۴۳ ریاضی هشتم
زاویههایی که درون یک چندضلعی قرار دارند، زاویههای داخلی آن چندضلعی نامیده میشوند. مجموع زاویههای داخلی یک مثلث ۱۸۰ درجه است.
| ۶ | ۵ | ۴ | ۳ | تعداد ضلعها |
| شکل | ||||
| ۴ | ۳ | ۲ | ۱ | تعداد مثلثها |
| ۷۲۰=۱۸۰°×۴ | ۵۴۰=۱۸۰°×۳ | ۲×۱۸۰°=۳۶۰° | ۱×۱۸۰°=۱۸۰° | مجموع زاویههای داخلی |
جدول بالا نشان میدهد که مجموع زاویههای داخلی یک چهارضلعی با مجموع زاویههای داخلی دو تا مثلث برابر است؛ پس مجموع زاویههای داخلی هر چهارضلعی ۳۶۰° میشود.
الف) با کامل کردن جدول، مجموع زاویههای داخلی چندضلعیهای دیگر را به دست آورید.
تعداد مثلت ها ۵ = ۲ – ۷
ب) فکر میکنید مجموع زاویههای داخلی یک هفت ضلعی چند درجه است؟
۹۰۰ = ۵ × ۱۸۰
تعداد مثلث ها ۶ = ۲ – ۸
یک هشت ضلعی چطور؟ چرا؟
۱۰۸۰ = ۱۸۰ × ۶
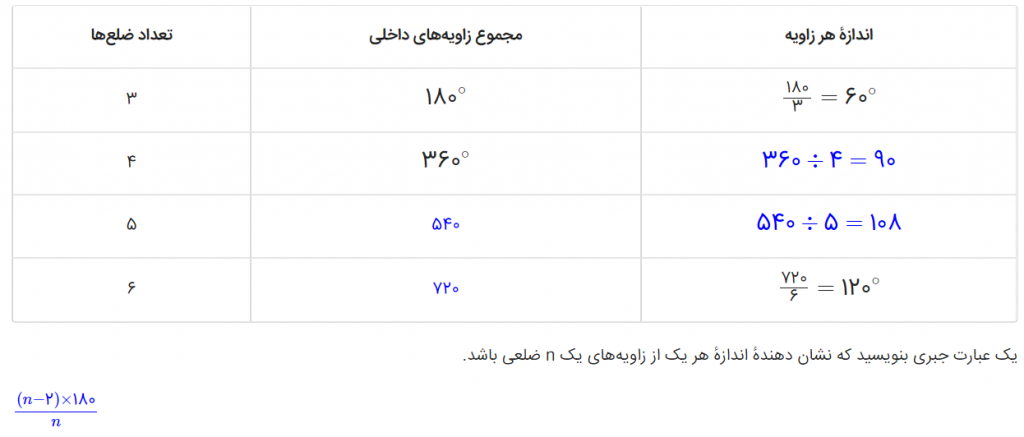
ج) عبارت جبری زیر را طوری کامل کنید که نشان دهنده مجموع زاویههای داخلی یک n ضلعی باشد.
۱۸۰° × (۲ – n) = مجموع زاویههای داخلی یک n ضلعی
اکنون با کامل کردن جدول زیر اندازهٔ هر یک از زاویههای داخلی چندضلعیهای منتظم را پیدا کنید.
گام به گام سایر صفحات زاویه های داخلی
- جواب صفحه ۴۲ ریاضی هشتم
- جواب فعالیت صفحه ۴۳ ریاضی هشتم
- جواب کار در کلاس صفحه ۴۴ ریاضی هشتم
- جواب تمرین صفحه ۴۵ ریاضی هشتم
برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
