جواب فعالیت صفحه ۱۰ هندسه دهم
در این نوشته با جواب فعالیت صفحه ۱۰ هندسه دهم همراه شما هستیم.
جواب فعالیت صفحه ۱۰ هندسه دهم
(برای مراحل زیر از خط کش و پرگار استفاده کنید.)
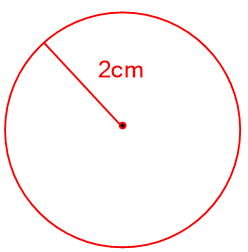
۱- نقطهای مانند O را در صفحه در نظر بگیرید و نقاطی را مشخص کنید که فاصلهٔ یکسانی از نقطهٔ O دارند. (مثلاً همهٔ نقاطی که فاصلهشان از نقطهٔ O برابر ۲ سانتی متر است.)
کافی است دایرهای به شعاع ۲ سانتیمتر رسم کنیم.
۲- خط d را در نظر بگیرید و تمام نقاطی که به فاصلهٔ ۲ سانتی متر از خط قرار d دارند را مشخص کنید.
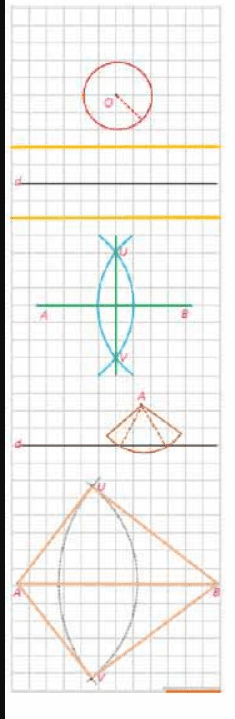
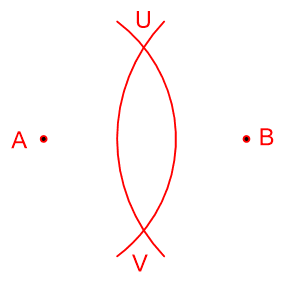
۳- نقاط A و B را در نظر بگیرید. دهانهٔ پرگار را بیش از نصف طول پاره خط AB باز کنید و یک بار به مرکز A و بار دیگر به مرکز B و با همان شعاع قبلی کمان بزنید تا یکدیگر را در نقاط V و U قطع کنند. V و U چه ویژگی مشترکی دارند؟
فاصله U از A با فاصله U از B برابر است و فاصلهی V از A با فاصلهی V از B برابر است.
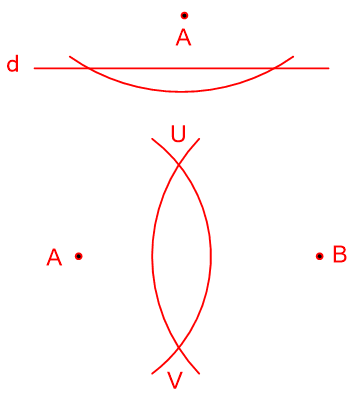
۴- نقطهٔ A، مانند شکل زیر به فاصلهٔ ۱ سانتی متر از خط d قرار دارد. نقاطی از خط d را بیابید که به فاصلهٔ ۲ سانتی متر از نقطهٔ A باشند.
کمانی به شعاع ۲ سانتیمتر و مرکز A رسم میکنیم. محل برخورد خط و کمان نقاط مورد نظر هستند.
۵- نقاط B و A را به فاصلهٔ ۵ سانتی متر از هم در نظر بگیرید. دهانهٔ پرگار را به اندازهٔ ۳ سانتی متر باز کنید و از نقطهٔ A یک کمان بزنید. سپس دهانهٔ پرگار را به اندازهٔ ۴ سانتی متر باز کنید و از نقطهٔ B یک کمان بزنید.
الف) نقاط روی کمان اول چه ویژگی مشترکی دارند.
فاصلهی همهی این نقاط از نقطهی A برابر با ۳ سانتیمتر است.
ب) نقاط روی کمان دوم چه ویژگی مشترکی دارند؟
فاصلهی همهی نقاط از نقطهی B برابر با ۴ سانتیمتر است.
پ) نقاط تقاطع دو کمان فاصلهشان از نقاط B و A چگونه است؟ برای اینکه چنین نقاط تقاطعی وجود داشته باشند، اندازهٔ شعاع آنها و فاصلهٔ نقاط B و A چه شرطی باید داشته باشند؟
فاصلهی نقاط تقاطع از A برابر با ۳ سانتیمتر و از B برابر با ۴ سانتیمتر است. برای اینکه چنین نقاط تقاطعی وجود داشته باشد باید حاصل جمع شعاعهای دو کمان از فاصلهی دو نقطهی A و B بیشتر باشد.
ت) طول اضلاع مثلث AUB چقدر است؟
۵ سانتیمتر= AB
۳ سانتیمتر= AU
۴ سانتیمتر= BU
برای مشاهده گام به گام سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «حالا درس» جست و جو کنید.
